leetcode热题100-GO-解-2025.3.24

23/100

今天的刷题就到这里，晚上复习下Java

238.除自身以外数组的乘积

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请 **不要使用除法，**且在 O(n) 时间复杂度内完成此题。

示例 1:

1
2
输入: nums = [1,2,3,4]
输出: [24,12,8,6]

示例 2:

1
2
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]

解一 第一思路解

分别计算前缀积和后缀积数组，再遍历相乘得出结果数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
func productExceptSelf(nums []int) []int {
	// 先判断特殊情况
	if len(nums) == 2 {
		return []int{nums[1], nums[0]}
	}
	n := len(nums)

	//初始化结果数组
	result := make([]int, n)
	//初始化前缀积数组和后缀积数组
	prefixProduct := make([]int, n)
	suffixProduct := make([]int, n)

	prefixProduct[0] = 1
	suffixProduct[n-1] = 1

	//计算前缀积
	for i := 1; i < n; i++ {
		prefixProduct[i] = prefixProduct[i-1] * nums[i-1]
	}

	//计算后缀积
	for i := n - 2; i >= 0; i-- {
		suffixProduct[i] = suffixProduct[i+1] * nums[i+1]
	}

	//计算结果数组
	for i := 0; i < n; i++ {
		result[i] = prefixProduct[i] * suffixProduct[i]
	}

	return result
}

解二 依然是采用前缀积和后缀积

但是优化空间复杂度，直接用结果数组存储前缀积，再另用变量存储当前后缀积，直接乘到结果数组上

空间复杂度优化到O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 依照解一的思路，我们可以发现，前缀积数组和后缀积数组是可以复用的
// 题目提示中有“出于对空间复杂度分析的目的，输出数组 不被视为 额外空间。”
// 所以我们可以直接使用结果数组来存储前缀积，再依次计算后缀积
func productExceptSelf2(nums []int) []int {
	// 先判断特殊情况
	if len(nums) == 2 {
		return []int{nums[1], nums[0]}
	}
	n := len(nums)
	//初始化结果数组
	result := make([]int, n)

	//计算前缀积
	result[0] = 1
	for i := 1; i < n; i++ {
		result[i] = result[i-1] * nums[i-1]
	}
	//直接复用结果数组累乘后缀积
	right := 1
	for i := n - 1; i >= 0; i-- {
		result[i] *= right
		right *= nums[i]
	}

	return result
}

41.缺失的第一个正数

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

示例 1：

1
2
3
输入：nums = [1,2,0]
输出：3
解释：范围 [1,2] 中的数字都在数组中。

示例 2：

1
2
3
输入：nums = [3,4,-1,1]
输出：2
解释：1 在数组中，但 2 没有。

示例 3：

1
2
3
输入：nums = [7,8,9,11,12]
输出：1
解释：最小的正数 1 没有出现。

忍不了了，直接哈希

但实际上空间复杂度不符合要求

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
// 直接用map解
func firstMissingPositive(nums []int) int {
	// 先判断特殊情况
	if len(nums) == 1 {
		if nums[0] == 1 {
			return 2
		} else {
			return 1
		}
	}
	n := len(nums)

	// 初始化map
	m := make(map[int]int, n)
	// 记录出现过的最大数
    maxN := 0
	for _, v := range nums {
		m[v]++
		if v > maxN {
			maxN = v
		}
	}

    // 实际上缺失的最小正整数只可能在(0,min(maxN, n)+1]区间内
	maxN = min(maxN, n)
    // 逐个遍历，看map中是否存在，若不存在则其为结果
	for i := 0; i < maxN; i++ {
		if _, ok := m[i+1]; !ok {
			return i + 1
		}
	}
    // 若maxN < 0，则自然为1
	if maxN < 0 {
		return 1
	}
    // 逐个遍历完都从[1,maxN]连续，结果自然为maxN+1
	return maxN + 1
}

解二 标准流程解

依照leetcode标准题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
// 原地哈希
func firstMissingPositive(nums []int) int {
	n := len(nums)
	// 先特况
	// 先判断特殊情况
	if n == 1 {
		if nums[0] == 1 {
			return 2
		} else {
			return 1
		}
	}

	// 遍历数组，将所有小于等于n的正整数放到对应位置
	for i := 0; i < n; i++ {
		// 因为是原地哈希，所以需要不断地将当前位置的数放到正确的位置
		// 所以需要使用for循环，直到当前位置的数放到正确的位置
		for nums[i] > 0 && nums[i] <= n && nums[nums[i]-1] != nums[i] {
			// 条件一 当前位置的数大于0小于等于n 这样才能放到正确的位置
			// 条件二 当前位置的数不在正确位置
			//    在原地哈希的情况下，对于nums[i] = x,将原数组视为哈希表
			//    则x应该放在nums[x-1]的位置
			//    所以nums[i]应该放在nums[nums[i]-1]的位置
			//    所以当nums[nums[i]-1]!= nums[i]时，当前位置的数不在正确位置
			//    交换位置 这里使用了Go的多重赋值（语法糖
			nums[nums[i]-1], nums[i] = nums[i], nums[nums[i]-1]
		}
	}

	// 遍历数组，找到第一个缺失的正整数
	for i := 0; i < n; i++ {
		if nums[i] != i+1 {
			return i + 1
		}
	}

	// 都正确则返回 n + 1
	return n + 1
}

解三 解二的变式

解二中是将有效正数的值放置在应有的位置上

即将nums[i] = x放放置在nums[x-1]

解三则为先处理所有无效数值

将所有原本的非正值和大于n的值置为n+1

即取最大的情况，缺少对应nums[n-1]的值n

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 三解 原地哈希，但用负值标记正整数匹配的位置
func firstMissingPositive(nums []int) int {
	n := len(nums)
	// 第一步：将所有小于等于 0 或者大于 n 的数置为 n + 1
	// 小于等于0默认无效，大于n的数也无效，因为缺失的第一个正数一定小于等于n+1，所以将其置为n+1
	for i := 0; i < n; i++ {
		if nums[i] <= 0 || nums[i] > n {
			nums[i] = n + 1
		}
	}

	// 第二步：标记出现过的正整数
	// 遍历数组，将每个出现过的正整数对应的位置上的数置为负数
	// 这里使用了绝对值，因为可能之前已经被置为负数了
	for i := 0; i < n; i++ {
		num := abs(nums[i])
		if num <= n {
			// 若小于n，即在有效范围内，就将正确位置的数置为负数
			//    即对nums[i] = x, 将x-1位置的数置为负数
			//    因为我们先排除了所有小于等于0或者大于n的数，所以num一定是有效值
			nums[num-1] = -abs(nums[num-1])
		}
	}

	// 第三步：找到第一个正数所在的位置
	for i := 0; i < n; i++ {
		if nums[i] > 0 {
			// 我们已经将有效正数应在的位置上的数置为负数
			// 所以第一个正数所在的位置i对应的正数i+1就是我们所求的结果
			return i + 1
		}
	}
	// 如果数组中所有位置都被标记为负数，说明 1 到 n 都出现过，返回 n + 1
	return n + 1
}

73.矩阵置零

给定一个*m x n* 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用**原地**算法。

示例 1：

img

1
2
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

img

1
2
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

  • m == matrix.length
  • n == matrix[0].length
  • 1 <= m, n <= 200
  • -231 <= matrix[i][j] <= 231 - 1

解一 空间复杂度O(m+n)
使用第一行和第一列来记录该行或该列是否有0
但是这样会导致第一行和第一列的信息被覆盖
所以需要额外的变量来记录第一行和第一列是否有0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func setZeroes(matrix [][]int) {
	// 先判断特殊情况
	m := len(matrix)
	n := len(matrix[0])
	if m == 1 && n == 1 {
		return
	}

	row := make([]bool, m)
	col := make([]bool, n)

	//遍历矩阵，记录需要置零的行和列
	for i := 0; i < m; i++ {
		for j := 0; j < n; j++ {
			if matrix[i][j] == 0 {
				row[i] = true
				col[j] = true
			}
		}
	}

	//再次遍历矩阵，根据记录的行和列信息进行置零
	for i := 0; i < m; i++ {
		for j := 0; j < n; j++ {
			if row[i] || col[j] {
				matrix[i][j] = 0
			}
		}
	}
}

解二 解一的优化 空间复杂度O(1)

实际上，我们并不关心第一行和第一列具体是哪个位置有0，我们只需要关注它是否有原生的0，即第一行和第一列本身是否需要置零

使用两个变量来单独存储此信息即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
// 二解 空间复杂度O(1)
// 使用第一行和第一列来记录该行或该列是否有0
// 但是这样会导致第一行和第一列的信息被覆盖
// 所以我们直接采用额外的两个变量来记录第一行和第一列是否有0，即是否最终也需要置零
// 这样就可以避免覆盖第一行和第一列的信息
func setZeroes(matrix [][]int) {
	// 先判断特殊情况
	m := len(matrix)
	n := len(matrix[0])
	if m == 1 && n == 1 {
		return
	}
	// 初始化变量
	firstRowZero := false
	firstColZero := false

	// 遍历第一行，记录第一行是否有0
	for j := 0; j < n; j++ {
		if matrix[0][j] == 0 {
			firstRowZero = true
			break
		}
	}
	// 遍历第一列，记录第一列是否有0
	for i := 0; i < m; i++ {
		if matrix[i][0] == 0 {
			firstColZero = true
			break
		}
	}

	// 遍历矩阵，记录需要置零的行和列
	for i := 1; i < m; i++ {
		for j := 1; j < n; j++ {
			if matrix[i][j] == 0 {
				matrix[i][0] = 0
				matrix[0][j] = 0
			}
		}
	}

	// 再次遍历矩阵，根据记录的行和列信息进行置零
	for i := 1; i < m; i++ {
		for j := 1; j < n; j++ {
			if matrix[i][0] == 0 || matrix[0][j] == 0 {
				matrix[i][j] = 0
			}
		}
	}

	// 根据额外变量的值，决定是否将第一行和第一列置零
	if firstRowZero {
		for j := 0; j < n; j++ {
			matrix[0][j] = 0
		}
	}
	if firstColZero {
		for i := 0; i < m; i++ {
			matrix[i][0] = 0
		}
	}
}

54.螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

img

1
2
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

img

1
2
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 10
  • -100 <= matrix[i][j] <= 100

解法没什么好说的，直接向四方向遍历，再更新四方向边界即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
func spiralOrder(matrix [][]int) []int {
	// 先判断特殊情况
	m := len(matrix)
	n := len(matrix[0])
	if m == 1 && n == 1 {
		return []int{matrix[0][0]}
	}

	// 初始化变量
	result := make([]int, 0, m*n)
	top, bottom, left, right := 0, m-1, 0, n-1

	for top <= bottom && left <= right {
		// 向右
		for j := left; j <= right; j++ {
			result = append(result, matrix[top][j])
		}
		top++

		// 向下
		for i := top; i <= bottom; i++ {
			result = append(result, matrix[i][right])
		}
		right--

		// 向左
		if top <= bottom {
			for j := right; j >= left; j-- {
				result = append(result, matrix[bottom][j])
			}
			bottom--
		}

		// 向上
		if left <= right {
			for i := bottom; i >= top; i-- {
				result = append(result, matrix[i][left])
			}
			left++
		}
	}

	return result
}

48.旋转矩阵

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在** 原地** 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

img

1
2
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

img

1
2
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

  • n == matrix.length == matrix[i].length
  • 1 <= n <= 20
  • -1000 <= matrix[i][j] <= 1000

抛开原题目约束，最方便也是最常规的方法是直接从数学上求解，直接乘个矩阵让其实现旋转90°的效果

或者对n*n矩阵，(i,j)元素，旋转后的位置为(j,n-1-i)

解一 可得出正确结果，但不满足题目要求

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
func rotateImage(matrix [][]int) {
	// 先判断特殊情况
	n := len(matrix)
	if n == 1 {
		return
	}

	// 创建一个新的矩阵来存储旋转后的结果
	newMatrix := make([][]int, n)
	for i := range newMatrix {
		newMatrix[i] = make([]int, n)
	}
	// 根据旋转规则将原矩阵元素复制到新矩阵
	for i := 0; i < n; i++ {
		for j := 0; j < n; j++ {
			newMatrix[j][n-1-i] = matrix[i][j]
		}
	}
	// 将新矩阵的元素复制回原矩阵
	for i := 0; i < n; i++ {
		for j := 0; j < n; j++ {
			matrix[i][j] = newMatrix[i][j]
		}
	}
}

解二 满足题目要求的标准解

先转置，再水平翻转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 二解 空间复杂度O(1)
// 直接原地旋转 先将图像沿着主对角线翻转，然后沿着水平轴翻转
func rotateImage2(matrix [][]int) {
	// 先判断特殊情况
	n := len(matrix)
	if n == 1 {
		return
	}

	// 沿着主对角线翻转
	for i := 0; i < n; i++ {
		for j := i + 1; j < n; j++ {
			matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
		}
	}

	// 沿着水平轴翻转
	for i := 0; i < n; i++ {
		for j := 0; j < n/2; j++ {
			matrix[i][j], matrix[i][n-1-j] = matrix[i][n-1-j], matrix[i][j]
		}
	}
}

240.搜索二维矩阵 II

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

  • 每行的元素从左到右升序排列。
  • 每列的元素从上到下升序排列。

示例 1：

img

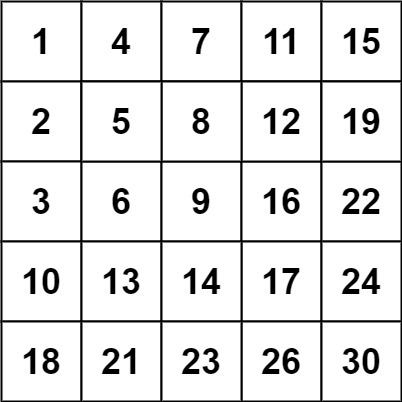
1
2
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

img

1
2
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= n, m <= 300
  • -109 <= matrix[i][j] <= 109
  • 每行的所有元素从左到右升序排列
  • 每列的所有元素从上到下升序排列
  • -109 <= target <= 109

关键点：从哪里入手能产生区分度？

​ 左上：向右或向下，matrix值都变大，无法区分

​ 右下：向左或向上，matrix值都变小，无法区分

​ 左下：向右变大，向上变小，可考虑

​ 右上：向左变小，向下变大，可以区分

实质上是将其理解为类似二叉搜索树

采取从右上开始遍历搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func searchMatrix(matrix [][]int, target int) bool {
	// 先判断特殊情况
	m := len(matrix)
	n := len(matrix[0])
	if m == 1 && n == 1 {
		return matrix[0][0] == target
	}

	// 从右上角开始搜索
	i, j := 0, n-1
	for i < m && j >= 0 {
		if matrix[i][j] == target {
			return true
		} else if matrix[i][j] < target {
			i++
		} else {
			j--
		}
	}
	return false
}

160.相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交**：**

img

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

直接考虑最佳方案 时间复杂度 O(m + n) 、仅用 O(1) 内存

采用双指针同时遍历两个链表

这两个链表分别为A+B和B+A

假设两个链表

1
2
A = a, b, c, x, d, e
B = f, g, h, i, j, k, x, d, e

则可以理解为我们在遍历

1
2
l1 = a, b, c, x, d, e, f, g, h, i, j, k, x, d, e
l2 = f, g, h, i, j, k, x, d, e, a, b, c, x, d, e

在存在相交的情况下，len(A) + offsetB == len(b) + offsetA是恒成立的

依照此逻辑，有以下代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
func getIntersectionNode(headA, headB *ListNode) *ListNode {
	if headA == nil || headB == nil {
		return nil
	}
	pA, pB := headA, headB
	// 当 pA 和 pB 不相等时继续遍历
	for pA != pB {
		if pA == nil {
			pA = headB
		} else {
			pA = pA.Next
		}
		if pB == nil {
			pB = headA
		} else {
			pB = pB.Next
		}
	}
	return pA
}

206.反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

img

1
2
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

img

1
2
输入：head = [1,2]
输出：[2,1]

示例 3：

1
2
输入：head = []
输出：[]

解一 迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
func reverseList(head *ListNode) *ListNode {
	// 先判断特殊情况
	if head == nil || head.Next == nil {
		return head
	}
	if head.Next.Next == nil {
		head.Next.Next = head
		newHead := head.Next
		head.Next = nil
		return newHead
	}

    //上一个节点
	prev := new(ListNode)
    //当前头结点的下一节点
	tmp := head.Next
    //GO中new出来的指针指向不为空，使用once保证第一次迭代时head.next指向nil
	once := true

	for tmp != nil {
		head.Next = prev
        //当前头的Next指向上一node
		if once {
            //首次迭代时指向nil
			head.Next = nil
			once = false
		}
        //更新上一指针指向已反转队列的头
		prev = head
        
        //更新head指向head.Next
		head = tmp
		tmp = tmp.Next
	}
	head.Next = prev
	return head
}

解二 递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func reverseList(head *ListNode) *ListNode {
	// 先判断是否递归结束
	if head == nil || head.Next == nil {
		return head
	}
    // 考虑递归到尽头时 newHead即为原list的endNode
	newHead := reverseList(head.Next)
    // 当前节点的Next指向上一层节点
	head.Next.Next = head
    // 上层节点的Next指向nil
	head.Next = nil
    // 处理完后，逐层返回原本的原本的endNode节点作为newHead返回
	return newHead
}