leetcode热题100-GO解-2025.4.1

49/100

简单广撒网写几题，然后复习下基本语法

基本语法真忘了（

108.将有序数组转换为二叉搜索树

水题

1
2
3
4
5
6
7
8
9
10
11
12
13
func sortedArrayToBST(nums []int) *TreeNode {
	if len(nums) == 0 {
		return nil
	}
	// 取数组中间元素作为根节点
	mid := len(nums) / 2
	root := &TreeNode{Val: nums[mid]}
	// 递归构建左子树
	root.Left = sortedArrayToBST(nums[:mid])
	// 递归构建右子树
	root.Right = sortedArrayToBST(nums[mid+1:])
	return root
}

94.二叉树的中序遍历

水题

前序/中序/后序 指 前根序/中根序/后根序

这三种只是改个顺序

另有层序遍历，这个得迭代做

1
2
3
4
5
6
7
8
9
10
11
12
// 前序/后序同理
func inorderTraversal(root *TreeNode) []int {
	if root == nil {
		return nil
	}
	// 递归遍历左子树
	left := inorderTraversal(root.Left)
	// 递归遍历右子树
	right := inorderTraversal(root.Right)
	// 合并结果
	return append(append(left, root.Val), right...)
}

104.二叉树的最大深度

水题

直接递归解掉刷过去不重要

1
2
3
4
5
6
7
8
9
10
11
func maxDepth(root *TreeNode) int {
	if root == nil {
		return 0
	}
	// 递归计算左子树的最大深度
	leftDepth := maxDepth(root.Left)
	// 递归计算右子树的最大深度
	rightDepth := maxDepth(root.Right)
	// 返回较大的深度
	return 1 + max(leftDepth, rightDepth)
}

226.翻转二叉树

水题

1
2
3
4
5
6
7
8
9
10
11
12
func invertTree(root *TreeNode) *TreeNode {
	if root == nil {
		return nil
	}
	// 交换左右子树
	root.Left, root.Right = root.Right, root.Left
	// 递归翻转左子树
	invertTree(root.Left)
	// 递归翻转右子树
	invertTree(root.Right)
	return root
}

101.对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

解一 递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func isSymmetric(root *TreeNode) bool {
	if root == nil {
		return true
	}
	// 递归检查左右子树是否对称
	return isMirror(root.Left, root.Right)
}

// 辅助函数：检查两个子树是否对称
func isMirror(left, right *TreeNode) bool {
	if left == nil && right == nil {
		return true
	}
	if left == nil || right == nil {
		return false
	}
	return left.Val == right.Val && isMirror(left.Left, right.Right) && isMirror(left.Right, right.Left)
}

解二 迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
func isSymmetric(root *TreeNode) bool {
	if root == nil {
		return true
	}

	// 初始化队列，将根节点的左右子节点入队
	queue := []*TreeNode{root.Left, root.Right}

	for len(queue) > 0 {
		// 从队列中取出两个节点
		left := queue[0]
		right := queue[1]
		queue = queue[2:]

		// 如果两个节点都为空，继续比较下一对节点
		if left == nil && right == nil {
			continue
		}

		// 如果其中一个节点为空，或者两个节点的值不相等，说明不对称
		if left == nil || right == nil || left.Val != right.Val {
			return false
		}

		// 将对称位置的节点对入队，以便后续比较
		queue = append(queue, left.Left, right.Right)
		queue = append(queue, left.Right, right.Left)
	}

	return true
}

543.二叉树的直径

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

实质上就是动态维护更新某个节点上的左右子树最大深度和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
func diameterOfBinaryTree(root *TreeNode) int {
	if root == nil {
		return 0
	}
	maxDiameter := 0
	var dfs func(node *TreeNode) int
	dfs = func(node *TreeNode) int {
		if node == nil {
			return 0
		}
		// 递归计算左子树的最大深度
		leftDepth := dfs(node.Left)
		// 递归计算右子树的最大深度
		rightDepth := dfs(node.Right)
		// 更新最大直径
		maxDiameter = max(maxDiameter, leftDepth+rightDepth)
		// 返回当前节点的最大深度
		return 1 + max(leftDepth, rightDepth)
	}
	dfs(root)
	return maxDiameter
}

102.二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

难以递归 使用迭代解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 迭代解法
// 实质上是维护了一个FIFO队列，一层层将当前节点取出，将其子节点入队
func levelOrder(root *TreeNode) [][]int {
	if root == nil {
		return nil
	}

	var result [][]int
	// 初始化队列
	queue := []*TreeNode{root}
	for len(queue) > 0 {
		levelSize := len(queue)
		var currentLevel []int
		for i := 0; i < levelSize; i++ {
			// 出队
			node := queue[0]
			queue = queue[1:]
			currentLevel = append(currentLevel, node.Val)
			// 若左子节点不为空，将其入队
			if node.Left != nil {
				queue = append(queue, node.Left)
			}
			// 若右子节点不为空，将其入队
			if node.Right != nil {
				queue = append(queue, node.Right)
			}
		}
		result = append(result, currentLevel)
	}
	return result
}

98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

  • 节点的左子树只包含 小于 当前节点的数。
  • 节点的右子树只包含 大于 当前节点的数。
  • 所有左子树和右子树自身必须也是二叉搜索树。

递归解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func isValidBST(root *TreeNode) bool {
	return isValidBSTHelper(root, nil, nil)
}

// 辅助函数：递归验证二叉搜索树
func isValidBSTHelper(root, min, max *TreeNode) bool {
	if root == nil {
		return true
	}
	// 若当前节点的值小于等于最小值，或大于等于最大值，返回 false
	if (min != nil && root.Val <= min.Val) || (max != nil && root.Val >= max.Val) {
		return false
	}
    // 对于左子树，当前节点为最大值
    // 对于右子树，当前节点为最小值
    // 递归往下传
	return isValidBSTHelper(root.Left, min, root) && isValidBSTHelper(root.Right, root, max)
}

230.二叉搜索树中第K小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

中序遍历

二叉搜索树的中序遍历是一个升序队列

依此维护一个LIFO栈每轮k--直至k == 0即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func kthSmallest(root *TreeNode, k int) int {
    var stack []*TreeNode
    for {
        // 遍历左子树，将节点入栈
        for root != nil {
            stack = append(stack, root)
            root = root.Left
        }
        // 取出栈顶元素
        root = stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        k--
        if k == 0 {
            return root.Val
        }
        // 转向右子树
        root = root.Right
    }
}

199.二叉树的右视图

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1：

**输入：**root = [1,2,3,null,5,null,4]

输出：[1,3,4]

解释：

img

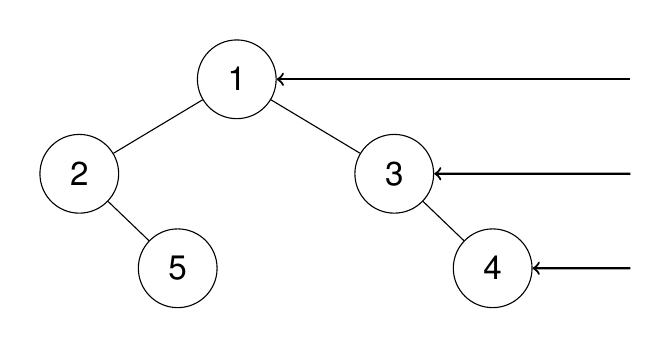
示例 2：

**输入：**root = [1,2,3,4,null,null,null,5]

输出：[1,3,4,5]

解释：

img

示例 3：

**输入：**root = [1,null,3]

输出：[1,3]

示例 4：

**输入：**root = []

输出：[]

思路：

采用层序遍历，当前层入栈完毕，遍历到当前栈最后一个节点时，将其加入结果数组中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func rightSideView(root *TreeNode) []int {
	var result []int
	if root == nil {
		return result
	}
	// 使用队列进行层序遍历
	queue := []*TreeNode{root}
	for len(queue) > 0 {
		levelSize := len(queue)
		// 遍历当前层的所有节点
		for i := 0; i < levelSize; i++ {
			node := queue[0]
			queue = queue[1:]
			// 如果是当前层的最后一个节点，将其值加入结果集
			if i == levelSize-1 {
				result = append(result, node.Val)
			}
			// 将左子节点加入队列
			if node.Left != nil {
				queue = append(queue, node.Left)
			}
			// 将右子节点加入队列
			if node.Right != nil {
				queue = append(queue, node.Right)
			}
		}
	}
	return result
}

114.二叉树展开为链表

这能标中等难度？？？

太水了有点

回过头手写考虑不周全好几次！！！

给你二叉树的根结点 root ，请你将它展开为一个单链表：

  • 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
  • 展开后的单链表应该与二叉树 先序遍历 顺序相同。

简单做一个递归先序遍历

中间用两个临时变量来做左右指针的转换就行

递归解法想明白就很简单

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func flatten(root *TreeNode) {
	if root == nil {
		return
	}
	// 递归展开左子树
	flatten(root.Left)
	// 递归展开右子树
	flatten(root.Right)

	// 保存原来的右子树
	right := root.Right
	// 将左子树移动到右子树的位置
	root.Right = root.Left
	root.Left = nil

	// 找到当前节点的右子树的最右边节点
	p := root
	for p.Right != nil {
		p = p.Right
	}
	// 将原来的右子树接在最右边节点的右边
	p.Right = right
}

解二 原地算法 迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
func flatten(root *TreeNode) {
	curr := root
	for curr != nil {
		if curr.Left != nil {
			// 找到左子树的最右节点
			pre := curr.Left
			for pre.Right != nil {
				pre = pre.Right
			}
			// 将原右子树接到左子树最右节点的右边
			pre.Right = curr.Right
			// 将左子树移动到右子树的位置
			curr.Right = curr.Left
			// 左子树置为空
			curr.Left = nil
		}
		// 移动到下一个节点继续处理
		curr = curr.Right
	}
}

46.全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

1
2
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

1
2
输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

1
2
输入：nums = [1]
输出：[[1]]

回溯算法！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func permute(nums []int) [][]int {
	var result [][]int
	var backtrack func(path []int, used []bool)
	backtrack = func(path []int, used []bool) {
		// 当路径长度等于原数组长度时，说明已经得到一个全排列
		if len(path) == len(nums) {
			temp := make([]int, len(path))
			copy(temp, path)
			result = append(result, temp)
			return
		}
		for i := 0; i < len(nums); i++ {
			// 如果该元素已经在路径中，跳过
			if used[i] {
				continue
			}
			// 选择当前元素
			path = append(path, nums[i])
			used[i] = true
			// 递归继续构建排列
			backtrack(path, used)
			// 回溯，撤销选择
			path = path[:len(path)-1]
			used[i] = false
		}
	}
	used := make([]bool, len(nums))
	backtrack([]int{}, used)
	return result
}