leetcode热题100-Java解-02

57/100

继续复习Java语法

437.路径总和 III

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

img

1
2
3
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

1
2
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

思路：

题目中提到，路径方向必须是向下的

采用前缀和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
private int ans = 0;

public int pathSum(TreeNode root, long targetSum){
    Map<Long, Integer> cnt = new HashMap<>();
    cnt.put(0L, 1);
    dfs(root, 0, targetSum, cnt);
    return ans;
}

private void dfs(TreeNode node, long s, long targetSum, Map<Long, Integer> cnt){
    if(node == null){
        return;
    }
    s += node.val;
    // 记录当前和
    ans += cnt.getOrDefault(s - targetSum, 0);
    // s == targetSum 时 cnt.get(0) = 1
    // <==> ans ++ 
    cnt.merge(s, 1, Integer::sum);
    // 
    dfs(node.left, s, targetSum, cnt);
    dfs(node.right, s, targetSum, cnt);
    cnt.merge(s, -1, Integer::sum);
}

从这题可以大体观出前缀和类解题模板

1
2
3
4
5
6
7
8
9
10
11
12
13
Map<Key, Integer> cnt;
// 用于记录前缀和
int sum = 0;

// 每到新的一个点时
sum += i;
// 尝试从前缀和map中取出 sum - target = n 的值
// 即 A -> B -> C -> ... -> F  = n
//    A -> B -> C -> ... -> F -> G -> H  = sum
//   cnt[sum - target] 即 cnt[n] 存在
//   等价于 有 G -> H = sum - n = target

//最后，若是在树等结构上遍历，节点回退时需要同时还原Map

236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

img

1
2
3
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

img

1
2
3
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

1
2
输入：root = [1,2], p = 1, q = 2
输出：1

解一 递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 解法一 递归
   private TreeNode ans;

   public Solution() {
       this.ans = null;
   }
   public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
       this.dfs(root, p, q);
       return this.ans;
   }

   private boolean dfs(TreeNode root, TreeNode p, TreeNode q) {
       if (root == null) return false;

       boolean lson = dfs(root.left, p, q);
       boolean rson = dfs(root.right, p, q);
       // 递归遍历子树，直到找到p或q

       if ((lson && rson) || ((root.val == p.val || root.val == q.val) && (lson || rson))) {
           // 满足最近公共祖先的条件：
           // 1. 左右子树分别包含p和q
           // 2. 当前节点是p或q，且左右子树中包含另一个节点
           ans = root;
       }

       // 返回当前子树是否包含p或q
       // 如果当前子树包含p或q，那么返回true
       // 对应的lson或rson也返回为true
       return lson || rson || (root.val == p.val || root.val == q.val);
   }

解二 Hashmap存储node.val -> parentNode 的映射关系

再用visited数组标记已访问的节点，求交叉

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 解法二 存储父节点
   public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
       Map<Integer, TreeNode> parent = new HashMap<Integer, TreeNode>();
       List<TreeNode> visited = new ArrayList<TreeNode>();
       this.dfs2(root, parent);
       while (p != null) {
           visited.add(p);
           p = parent.get(p.val);
       }
       while (q != null) {
           if (visited.contains(q)) {
               return q;
           }
           q = parent.get(q.val);
       }
       return null;
   }

   public void dfs2(TreeNode root, Map<Integer, TreeNode> parent) {
       if (root == null) {
           return;
       }
       if (root.left != null) {
           parent.put(root.left.val, root);
           dfs2(root.left, parent);
       }
       if (root.right != null) {
           parent.put(root.right.val, root);
           dfs2(root.right, parent);
       }
   }

124.二叉树中的最大路径和

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

img

1
2
3
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

img

1
2
3
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

个人感觉上是有些类似于前缀和/后缀和的思想

标准的解法是递归，为每个节点计算以该节点为根由上至下的最大序列和作为其贡献值

leftGain/rightGain < 0 时，直接抛弃，取0值

以当前节点为根的最大路径和为priceNewpath = node.val + leftGain + rightGain

再尝试更新全局最大值

递归返回当前节点最大贡献值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 递归
int maxSum = Integer.MIN_VALUE;
   public int maxPathSum(TreeNode root) {
       maxGain(root);
       return maxSum;
   }
   public int maxGain(TreeNode node) {
       if (node == null) {
           return 0;
       }
       // 递归计算左右子节点的最大贡献值
       // 只有在最大贡献值大于 0 时，才会选取对应子节点
       int leftGain = Math.max(maxGain(node.left), 0);
       int rightGain = Math.max(maxGain(node.right), 0);
       // 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
       int priceNewpath = node.val + leftGain + rightGain;
       // 更新答案
       maxSum = Math.max(maxSum, priceNewpath);
       // 返回节点的最大贡献值
       return node.val + Math.max(leftGain, rightGain);
   }

200.岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

1
2
3
4
5
6
7
输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

1
2
3
4
5
6
7
输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 网格dfs算法
	public int numIslands(char[][] grid) {
        if (grid == null || grid.length == 0) {
            return 0;
        }

        int nr = grid.length;
        int nc = grid[0].length;
        int num_islands = 0;
        for (int r = 0; r < nr; ++r) {
            for (int c = 0; c < nc; ++c) {
                if (grid[r][c] == '1') {
                    ++num_islands;
                    dfs(grid, r, c);
                }
            }
        }

        return num_islands;
    }

    void dfs(char[][] grid, int r, int c) {
        int nr = grid.length;
        int nc = grid[0].length;
        if (r < 0 || c < 0 || r >= nr || c >= nc || grid[r][c] == '0') {
            return;
        }

        // 因为只要统计数量，所以把遍历过的1都置为0
        grid[r][c] = '0';
        dfs(grid, r - 1, c);
        dfs(grid, r + 1, c);
        dfs(grid, r, c - 1);
        dfs(grid, r, c + 1);
    }

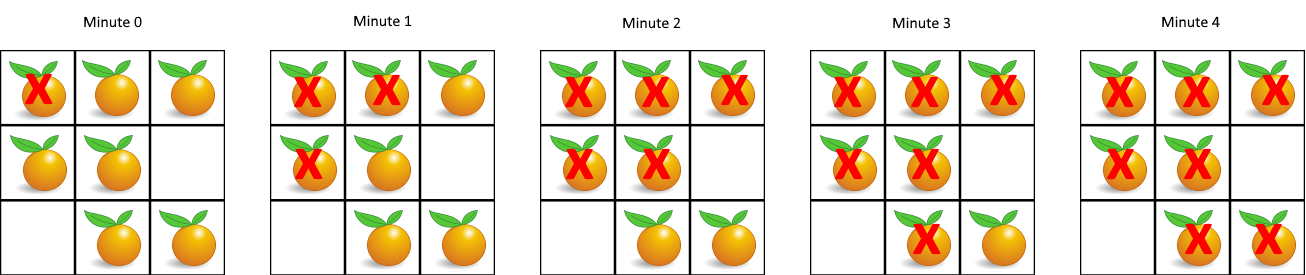
994.腐烂的橘子

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

  • 值 0 代表空单元格；
  • 值 1 代表新鲜橘子；
  • 值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

img

1
2
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

1
2
3
输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。

示例 3：

1
2
3
输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

思路：

广度优先搜索 类似二叉树层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
public int orangesRotting(int[][] grid) {
       int rows = grid.length;
       int cols = grid[0].length;
       // 用于存储腐烂橘子的队列
       Queue<int[]> queue = new LinkedList<>();
       // 新鲜橘子的数量
       int freshOranges = 0;
       // 四个方向：上、下、左、右
       int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};

       // 遍历网格，将腐烂的橘子加入队列，统计新鲜橘子的数量
       for (int i = 0; i < rows; i++) {
           for (int j = 0; j < cols; j++) {
               if (grid[i][j] == 2) {
                   queue.offer(new int[]{i, j});
               } else if (grid[i][j] == 1) {
                   freshOranges++;
               }
           }
       }

       // 如果没有新鲜橘子，直接返回 0
       if (freshOranges == 0) {
           return 0;
       }

       int minutes = 0;
       // 进行 BFS
       while (!queue.isEmpty()) {
           int size = queue.size();
           boolean hasRotten = false;
           for (int i = 0; i < size; i++) {
               int[] current = queue.poll();
               int x = current[0];
               int y = current[1];
               // 遍历四个方向
               for (int[] dir : directions) {
                   int newX = x + dir[0];
                   int newY = y + dir[1];
                   // 检查新位置是否合法且为新鲜橘子
                   if (newX >= 0 && newX < rows 
                       && newY >= 0 && newY < cols 
                       && grid[newX][newY] == 1) {
                       
                       // 将新鲜橘子标记为腐烂
                       grid[newX][newY] = 2;
                       // 新鲜橘子数量减 1
                       freshOranges--;
                       // 将新的腐烂橘子加入队列
                       queue.offer(new int[]{newX, newY});
                       hasRotten = true;
                   }
               }
           }
           // 如果有橘子腐烂，时间加 1
           if (hasRotten) {
               minutes++;
           }
       }

       // 如果还有新鲜橘子，返回 -1
       return freshOranges == 0 ? minutes : -1;
   }